| Et maintenant pour achever:
3°) Association de bicyls et de sphérocyls à axes croisés
Une très longue démonstration prend pour origine la valeur
approchée oblique des vergences principales.
Pour un méridien faisant un angle j
avec l'axe du cylindre de vergence D, sa puissance s'exprime par l'égalité
D'= DSin²j.
Dans l'axe: j =0, Sinj
= 0, D' = D = 0. Dans le contraxe: j = 90°
; Sinj =1 —› D '= D.
Cette démonstration aboutit à la construction vectorielle
suivante:
Soit à associer deux plancyls C1 à
a1° T.A.B.O. Et C2
à a2°
T.A.B.O.
a) Transposer les cylindres afin qu'ils soient exprimés dans le
même signe.
b) Tracer un repère orthonormé.
c) Choisir pour C1 celui dont l'axe est le plus
proche de 0° T.A.B.O.
d) Tracer le vecteur d'une longueur proportionnelle à C1,
faisant un angle a1°,
avec le 0° du repère orthonormé . (choisir une échelle
rendant le schéma lisible)
e)Tracer un deuxième vecteur d'une longueur proportionnelle à
C2, faisant avec C1, un angle
2a
où a =
(a2 - a1).
f)Le cylindre résultant Cr est la composante vectorielle des vecteurs
C1 et C2.
g) l'axe du cylindre Cr résultant est la bissectrice de l'angle
2q compris entre C1
et Cr.
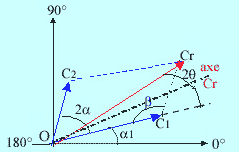 
Nous pouvons calculer, la valeur numérique du cylindre résultant
qui a même signe que celui des deux cylindres composés. L'axe
du cylindre résultant a pour valeur dans le schéma T.A.B.O.
j = a1
+ q
Une variante permet de déterminer q
à partir de son sinus:
Sin2 q = C2
x Sin2a.
C1
Cependant comme Sin2q = Sin (180°-
2q), un schéma non fait ou
incertain, peut entraîner des erreurs. Alors que
Cos2q = - Cos (180°- 2q).
Plus aisé à repérer entre 0° et 180°.
A tout cela, il faut ajouter que la combinaison de cylindres entraîne
une sphère résultante dans l'égalité:
sr = C1 + C2 - Cr
2
Pour associer des sphérocyls, on les transposera dans des cylindres de
même signe, puis on composera uniquement les cylindres pour obtenir le
cylindre résultant en valeur et axage. Après avoir calculé la valeur de
la sphère résultante, on l'additionnera aux deux sphères constituant les
sphérocyls transposés. S = S1+ S2
+ sr (Attention aux erreurs de signe). Si un examen optométrique se présente
en axes croisés, le réflexe élémentaire sera de poser la lunette d'essai
sur le frontofocomètre et de lire directement les vergences principales
résultant de la combinaison.(À quoi ça sert que Monsieur Essilor
se décarcasse!). Nous pourrions démontrer également dans ce chapitre
que lorsqu'une lentille épaisse est surfacée avec un dioptre arrière torique
, l'astigmatisme du dioptre torique est égal à l'astigmatisme de la lentille.
Alors qu'en dioptre torique avant, cette égalité n'est qu'approximative. |