EPAISSEURS DES LENTILLES
VERGENCES DES DIOPTRES

I EPAISSEURS DES LENTILLES
II VERGENCES DES DIOPTRES
III RAPPORT ENTRE LES VERGENCES D'UNE LENTILLE

I EPAISSEURS DES LENTILLES
Il nous intéresse de connaître diverses épaisseurs au centre ou au bord de lentille selon leur indice, leur vergence et leur forme. Certains logiciels de fabricants peuvent dès la commande nous renseigner sur ces épaisseurs ainsi que le poids des lentilles commandées. Il demeure culturel de connaître l'origine de ces résultats.

La flèche d'un dioptre de rayon R, est la hauteur f de la calotte sphérique limitée par une base AB de grandeur déterminée 2h.
- Dans une lentille ménisque convexe l'épaisseur au centre nous importe le plus: Ec = f1 - f2 + eb
- Pour une lentille biconcave: Eb = f1 + f2 + ec
- Pour une lentille ménisque concave, L'épaisseur au bord nous importe le plus: Eb = f2 - f1 + ec
On constate qu'il s'agit de la même égalité que pour une lentille ménisque convexe présentée différemment.
- Pour une lentille biconvexe: Ec = f1+ f2 + eb
Il s'agit maintenant d'établir une relation entre le rayon de courbure du dioptre et l'intervalle qui sépare le centre optique d'un point de la lentille.

Le flèche est représentée par S1H = f ; posons h = AB/2 ; S1S' = 2R ( R est le rayon de courbure du dioptre dans le triangle concerné). Dans le traingle AHC on peut écrire:
AC² = AH² + HC² ; HC = R - f —> R² = h² + (r - f)² —> R² = h² + R² -2Rf + f² —> h² = 2Rf - f²
h est l'intervalle qui sépare le centre optique d'un point quelconque d'une lentille ophtalmique mais plus particulièrement un point du périmètre de la lentille calibrée aux cotes d'une monture.
L'approximation de Rayleigh juge que f²est négligeable par rapport à 2Rf et l'égalité devient h² = 2Rf d'où f = h²/2R.
Cette approximation est suffisante pour les élèves de BEP ( voir référenciel). Elle ne sera admise en BTS que dans la mesure où l'énoncé d'un exercice l'autorise.Sans cette approximation l'égalité devient h² -2Rf + f² = 0.Elle possède deux racines :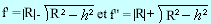 La valeur f ' qui correspond à S1H est celle recherchée; f " correspond à HS'. Inutile dans le calcul des flèches d'un dioptre, elle peut être utilisée dans le calcul des dimensions de la pastille d'une lentille bi ou trifocale.
II VERGENCES DES DIOPTRES
1°) Sphéromètre
Un sphéromètre est un appareil qui comporte trois pointes fixes réparties selon un triangle équilatéral et une pointe mobile située au centre du cercle circonscrit à ce triangle. Si on applique le sphéromètre sur un dioptre sphérique, le déplacement de la pointe centrale, par rapport aux trois pointes fixes, mesure la flèche de la calotte limitée par le cercle circonscrit défini par les trois pointes fixes. Son déplacement est proportionnel à la vergence du dioptre étudié. Un engrenage permet de lire directement la vergence de ce dioptre. On remarquera que chaque sphéromètre est étalonné en fonction d'un indice de verre et qu'une conversion sera nécessaire pour la détermination de la vergence d'un dioptre si son indice n'est pas identique à celui de l'étalonnage de l'appareil. La condition de proportionnalité induit une erreur relative moyenne de 1/8 d

2°) Cylindromètre
Un cylindromètre est un appareil du même type que le sphéromètre avec deux pointes fixes situées symétriquement de part et d'autre d'une pointe mobile. Son déplacement détermine la dimension d'une flèche et par conséquent la vergence d'un dioptre. Cet appareil convient pour la mesure d'un dioptre cylindrique et d'un méridien d'un dioptre torique. Pour la mesure des dioptres sphériques il est nécessaire de bien positionner la pointe mobile au sommet de la calotte du dioptre.

III RAPPORTS ENTRE LES VERGENCES D'UNE LENTILLE
Si un lentille est considérée comme mince au centre, la vergence frontale image est identique à la vergence sphérométrique Ds = D'f = D1 + D2. Cette condition n'est tolérable que pour des lentilles de vergences inférieures à + 2d. Dans les autres cas il faudra tenir compte de l'épaisseur au centre de la lentille. La méthode la plus directe, consiste à exprimer que le foyer image F' de la lentille est l'image du foyer image F'1 du premier dioptre D1 donnée par le second dioptre D2

Cette égalité établit une relation entre les différentes vergences d'une lentille et son épaisseur au centre. On remplacera directement les éléments connus par leurs valeurs numériques pour calculer l'élément recherché. On notera que si les vergences des dioptres sont exprimées en dioptrie, l'épaisseur au centre sera exprimée en mètre.
Remarque: Cette méthode est parfois appelée méthode des foyers. Mais il faut rendre à Descartes ce qui revient à Descartes . Alors appelons la par exemple: association de Descartes rapportée aux foyers.

COMPLEMENT:
Pour quel diamètre une lentille ménisque convexe, d'épaisseur au centre ec est-elle à bord tranchant (eb = 0)?
On pose :
a) ec = f1 - f2 ou f1 =ec + f2
b) h² = 2R1f1 - f1² = 2R2f2 - f2²
en remplaçant f1 dans b)
2R1(ec + f2) - (ec + f2)² = 2R2f2 - f2² ;
2R1ec + 2R1f2 - ec² - 2ecf2 -f2² = 2R2f2 - f2²
2R2f2 -2R1f2 + 2ecf2 = 2R1ec - ec²
                          f2 =  2R1ec - ec²
                                2(R2 - R1 + ec)
On démontrerai de même que pour une lentille biconvexe:
                           f2 =   2R1ec - ec²
                                2( R2 + R1 - ec)
On remplace dans b) f2 par sa valeur pour calculer h² et h et trouver le diamètre de la lentille à bord tranchant égal à 2h

EXERCICE (correction par mail)
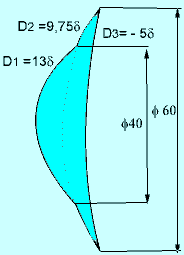
 Une lentille organique de type lenticulaire à bord tranchant (eb =0) d'indice n =1,523 possède les caractéristiques ci-dessous.
1°) Calculer sa vergence commerciale. (arrondie au ¼ de dioptrie).
2°) Calculer l'épaisseur au bord d'une lentille ménisque de dioptres avant et arrière identique à la lentille précédente et d'épaisseur au centre ec = 6mm
3°) Conclusions. Avantages et inconvénients de ces lentilles. Quelle autre type de lentille était envisageable ?