lentilles sphériques

I DEFINITIONS
On appelle verres sphériques, des lentilles dont les deux dioptres sont des calottes de sphère ou un des dioptres est sphérique et l'autre plan. On distingue trois catégories : les lentilles convergentes ou convexes (Cx, +), les lentilles divergentes ou concaves (Cc, -) et les lentilles afocales (plan). En lunetterie, une lentille en matière minérale peut avoir un indice de 1,523 ; 1,602; 1,7; 1,8; 1,9 et parfois supérieur à 2. En matière organique elle peut avoir un indice de 1,498 ;1,502; 1,561. Sa forme est presque toujours celle d'un ménisque dont la face convexe est obligatoirement tournée vers la lumière.

On appelle axe optique la droite qui joint les centres de courbures C1 et C2 des dioptres. S1 et S2 appelés sommets sont les points de concours de l'axe optique avec les dioptres D1 et D2.
II VERGENCES
a) Vergences des dioptres Le dioptre avant D1 a toujours une vergence positive. Le dioptre arrière D2 a toujours une vergence négative. Si dans un exercice, on énonce: "un dioptre arrière de 3dioptries " c'est obligatoirement - 3dioptries qu'il faudra comprendre. Soient R1 et R2 les valeurs arithmétiques des rayons de courbures et n l'indice du verre, la vergence des dioptres s'exprime par les égalités:

D1 = n -1 et D2 = 1 - n La lentille étant dans le milieu air: n' =1(sauf pou les pêcheurs sous- marin )
R1 R2

b) Vergence cardinale, vraie, de Gauss... Soit une lentille épaisse de deux dioptres sphériques D1 et D2 séparés par une distance S1 S2 = ec , la vergence focale D est donnée par la formule d'association de Gullstrand:

D = D1+ D2 - ec D1 x D2
n
et la positionsdes plans principaux: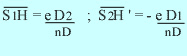 et

c)Vergence frontale image:
En lunetterie quand on parle de vergence, c'est d'elle dont il s'agit. C'est celle qui est indiquée sur la pochette des fabricants. La vergence frontale image est la proximité du plan focal image F' à partir du sommet S2 :
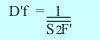; par analogie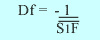
d)Vergence sphérométrique:
elle suppose l'épaisseur au centre négligeable Ds = D'f = D = D1 + D2

III APPLICATIONS EN LUNETTERIE
1°) Types de lentilles
a) Les lentilles biconvexes, ou biconcaves ne sont guère utilisées de nos jours. On les rencontre dans les boîtes d'essais ou sous la forme de loupes. La vision n'est nette qu'aux alentours du centre optique.
b) Les lentilles ménisques. De moins en moins utilisées sous leur forme générique, elles ont un dioptre convexe et un dioptre concave. Le convexe est toujours tourné vers la lumière.
c) Les lentilles ponctuelles.
Elles furent calculées par Tscherning (1906) qui montre qu'il est possible de conserver une astigmatisme encore tolérable, pour des rayons obliques à 0° et 30°, pour des corrections allant de - 20d à +7d. Il détermine les courbures de surfaçage des dioptres grâce à une ellipse. Jusqu'aux années 1990, les lentilles étaient stockées chez les fabricants sous forme de semi-finis. Un dioptre était surfacé selon une base issue des calculs de Tscherning pour obtenir une lentille de qualité optimum. Par exemple, pour une lentille finie de vergence + 8d, le dioptre de base avait une vergence de - 3d (dioptre concave). Maintenant, les semi-finis sont stockés selon des dioptres de référence de surfaçage convexes. Si les lentilles issues des calculs de Tscherning convenaient pour des petits diamètres, elles sont inadaptées à l'heure actuelle, car trop cambrées pour les lentilles de grands diamètres. Les fabricants ont modifié les courbures tout en restant proches de celles définies par l'ellipse de Tscherning.
d) Lentilles asphériques.
Leur genèse, sous forme de prismes date de Fresnel (inventeur du phare breton). Il souhaitait obtenir un faisceau de lumière parallèle pour avoir un éclairage en mer le plus efficace possible. Son procédé diminua les aberrations sphériques. Dans les années 70, la chirurgie a permis la banalisation des opérations de la cataracte. La vergence des lentilles correctrices dépassait les +12d, donc bien au-delà des + 7d de Tscherning, il s'en suivait de mauvaises conditions de vision latérale (effet de couloir) puis les lentilles de type lenticulaire de plus petit diamètre efficace provoquaient des scotomes annulaires peu confortables. Les progrès dans les calculs de surface grâce aux ordinateurs ont permis le surfaçage de lentilles asphériques dont les vergences varient selon les coordonnées géographiques de la lentille et de corriger ainsi efficacement les aphaques. L'évolution vers les implants a ralenti le marché pour ce type de corrections, mais le surfaçage asphérique a été étendu aux autres lentilles quelles que soient leurs vergences. En gagnant en platitude des dioptres (grâce également aux nouveaux indices) et en épaisseur, il a été possible d'associer esthétisme et confort visuel par corrections des aberrations sphériques et des faisceaux obliques.

2°) Normalisations et tolérances
a) Normalisations des vergences
Elle est de 0, 25 d en 0, 25 d jusqu'à ± 6,00 d
Elle est de 0, 50 d en 0, 50 d jusqu'à ± 14,00 d
Elle est de 1, 00 d en 1, 00 d au-delà
Il est à noter qu'avec les progrès de la technique cette normalisation est obsolète et que la notion d'intercourbe a presque disparu.
b) Les diamètres ne sont pas normalisés. La coutume les fait varier de 5mm en 5mm jusqu'à 85 mm.
c)Tolérances de fabrication
de plan à ± 5,00d = ±1/16d
de ± 5,50d à ± 12,00d = ±1/8d
de ± 12,50 d et au-delà = ±1/4d
Exemples: 3,94d < 4d < 4,06d ; 7,88d < 8d < 8,12d ; 13,75 d < 14 d < 14, 25d
La tolérance pour ce dernier cas rend illusoire un échelonnement dans les prescriptions de 0, 25d en 0, 25d.
d) tolérance de centrage
Le centre optique ou le centre de montage coïncide avec le centre géométrique de la lentille à 0,5 mm près